大阪大学 大学院人間科学研究科 行動統計科学研究分野

Recent Studies

Studies since 2012

Notation common among several procedures

X:  n-observations×p-variables column-centered data matrix

S:  p-variables×p-variables sample covariance matrix

F:  n-observations×m-factors score matrix, F’F = nI (identity matrix)

A:  p-variables×m-factors loading matrix, m ≤ min(n, p)

U:  n-observations×p-variables score matrix, U’U = nI, F’U = O (zero matrix)

Ψ:  p-variables×p-variables diagonal matrix

Factor Analysis (FA)

  1. Matrix Decomposition FA: Algorithm for min F, A, U, Ψ ||X–FA’-UΨ||2 to obtain A and U only from S (Adachi, 2012).
  2. EM Algorithm: Proving that it cannot give improper solutions (Adachi, 2013).
  3. Sparse FA: min F, A, U, Ψ||X–FA’-UΨ||2 s.t. Cardinality(A)=const., without using penalties (Adachi & Trendaifilov 2015).
  4. Generalized Least Squares Method: min A, Ψ tr{(S–AA’-Ψ2)Ψ–2}2 using majorization (Adachi, 2015).
  5. Caregorical FA: min F, A, U, Ψ, Q Σj||GjQj–FAj‘–UjΨj||2 s.t. Qj‘Gj‘GjQj = nI, GkQk being column-centered with Gk n-observations×Kj-categories membership indicator matrix (Makino, 2015).
  6. Clustering FA: min F, A, Ψ nlog|Ψ2|+ tr(X–GCA’)Ψ–2(X–GCA’)’ s.t. F = GC with G an n×g membership matrix (Uno, Satomura, & Adachi, 2016).

Principal Component Analysis (PCA)

  1. Generalized Joint Procrustes Analysis: min N, F, A Σk(n–1||FkNk–F||2+ p–1||AkNk–1–A||2) with Xk≅FkAk‘=FkNkNk–1Ak‘ (Adachi, 2015).
  2. Sparse PCA: min F, A ||X–FA’||2 over F, A s.t. Cardinality(A)=const. (Adachi & Trendaifilov 2016).
  3. SparseTucker2: min F, A ||Z–FH(I⊗M’)||2 s.t. Cardinality(H)=const. with the slices of three-way data horizontally arranged in Z (Ikemoto & Adachi, 2016).

Canonical Correlation Analysis

  1. Reformulation: as　maxA,B tr{XA(A’X’XA)–1A’X’}{YB(B’Y’YB)–1B’Y’} s.t. rank(XA)=rank(YB)≤ min(p,q) is proved, which allows oblique rotation, with [X, Y] an n × (p+q) data matrix (Satomura & Adachi, 2013).

References: clich Here

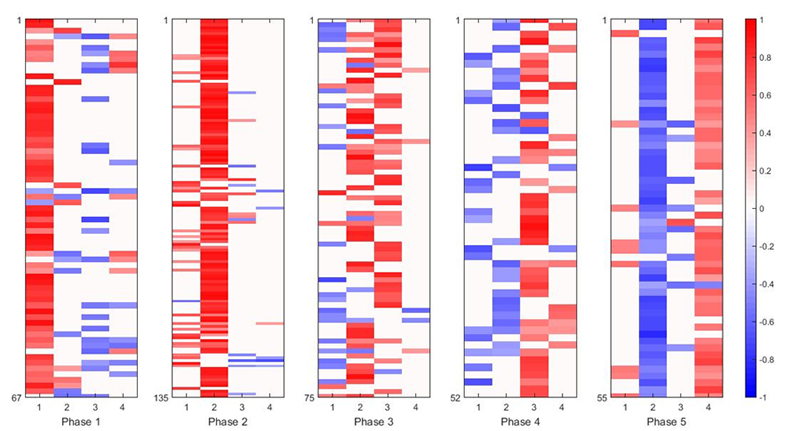
Resulting A in [8] for gene expression data

PAGE TOP