大阪大学 大学院人間科学研究科 行動統計科学研究分野

「最近の研究開発」のページは現在準備中です

最近の研究開発（2021年度までの内容）

2012年以降の研究開発:開発手法は定式化で，理論研究は一文で要約

複数手法に共通する記号

X:  n個体×p変数の列中心化されたデータ行列

S:  p変数×p変数の標本共分散行列

F:  n個体×m因子の得点行列, F’F = nI (単位行列)

A:  p変数×m因子の負荷行列, m ≤ min(n, p)

U:  n個体×p変数の得点行列, U’U = nI, F’U= O (零行列)

Ψ:  p変数×p変数の対角行列

因子分析

  1. 行列因子分析の解法: min F, A, U, Ψ ||X–FA’-UΨ||2のA, Ψの解を，Sだけから求めるアルゴリズム (Adachi, 2012).
  2. EMアルゴリズム: 不適解を与えないことを証明 (Adachi, 2013).
  3. スパース因子分析: min F, A, U, Ψ||X–FA’-UΨ||2 s.t. Aの零要素数=定数. ペナルティを使わないのが特徴 (Adachi & Trendaifilov 2015).
  4. 一般化最小二乗法: Majorizationを使ったmin A, Ψ tr{(S–AA’-Ψ2)Ψ–2}2 (Adachi, 2015).
  5. カテゴリカル因子分析: min F, A, U, Ψ, Q Σj||GjQj–FAj‘–UjΨj||2 s.t. Qj‘Gj‘GjQj=nI, GkQkは列中心化．ここで，Gkはn個体×Kjカテゴリーのメンバーシップデータ行列　(Makino, 2015).
  6. クラスタリング因子分析: min F, A, Ψ nlog|Ψ2|+ tr(X–GCA’)Ψ–2(X–GCA’)’ s.t. F=GC. ここで，G はn個体×g群の未知メンバーシップ行列 (Uno, Satomura, & Adachi, 2016).

主成分分析

  1. 一般化同時プロクラステス分析: min N, F, A Σk(n–1||FkNk–F||2+p–1||AkNk–1–A||2).
    ここで，Xk≅FkAk‘=FkNkNk–1Ak‘ (Adachi, 2015).
  2. スパース主成分分析: min F, A ||X–FA’||2 over F, A s.t. Aの零要素数=定数 (Adachi & Trendaifilov 2016).
  3. スパースTucker2: min F, A ||Z–FH(I⊗M’)||2 s.t. Hの零要素数=定数. ここで，Zは三相データのスライスを横に並べた行列 (Ikemoto & Adachi, 2016).

正準相関分析

  1. 再定式化:　maxA,B tr{XA(A’X’XA)–1A’X’}{YB(B’Y’YB)–1B’Y’} s.t. rank(XA)=rank(YB)≤min(p, q)と定式化できること(斜交回転可能)を証明. ここで, [X, Y]はn ×(p+q)のデータ行列 (Satomura & Adachi, 2013).

文献はこちらをクリック

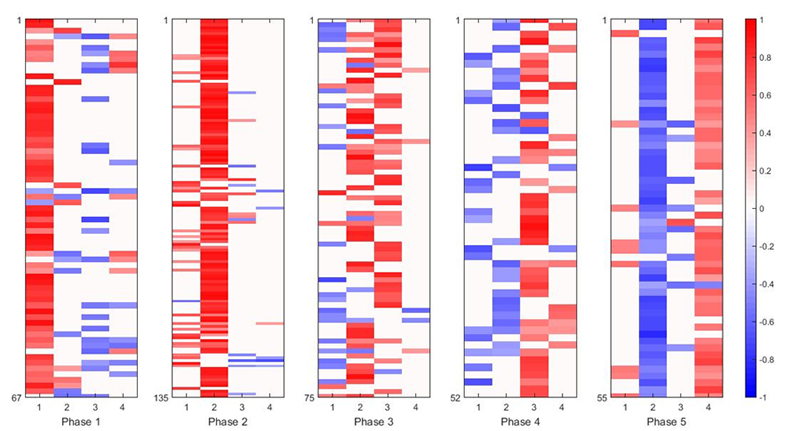
遺伝子表現データに対する[8]のAの解

PAGE TOP